Regresores: conociendo al hermano pequeño de las redes neuronales#

Nuestros primeros pasos por el camino de baldosas amarillas nos llevan al hermano pequeño de la familia de redes neuronales: el regresor logístico, al que, en general, ni siquiera se considera una red neuronal. Por el camino, aprenderás muchos elementos del aprendizaje automático que luego seguirán aplicándose a modelos más complejos.

Nota

Esta página es parte de la serie "Un recorrido peso a peso por el transformer", donde se presenta una guía para aprender cómo funcionan las redes neuronales que procesan textos y cómo se programan. Es también posible que hayas llegado a ella desde otra fuente (por ejemplo, una asignatura específica) que plantee otra forma diferente de utilizar estos contenidos. En ese caso, usa las recomendaciones y la planificación que te ofrezca esa fuente.

Regresores#

Estudia este tema con el capítulo "Logistic Regression" del libro de Jurafsky y Martin, complementándolo con lo que se discute más abajo.

Casi la totalidad del capítulo es muy relevante para nuestros propósitos al tratarse de un capítulo introductorio, pero puedes saltarte lo siguiente:

La introducción que hay antes del apartado 5.1, ya que se basa en elementos de capítulos anteriores (clasificador bayesiano) que no has visto.
El apartado 5.2.2 ("Other classification tasks and features").
El apartado 5.2.4 ("Choosing a classifier").
La sección 5.7 ("Regularization").
Por último, no es necesario que comprendas la sección 5.10 ("Advanced: Deriving the Gradient Equation") antes de pasar a capítulos posteriores, pero es muy recomendable que seas capaz de derivar por ti mismo la función de pérdida más pronto que tarde. Cuando los modelos se vayan haciendo más complejos, obtener la derivada manualmente será una tarea ardua e innecesaria (porque librerías como PyTorch se encargarán de calcularla por nosotros), pero hacerlo ahora mejorará tu perspectiva del entrenamiento de redes neuronales.

Este capítulo puede que resulte ser de los más complejos y el que ofrece una mayor curva de aprendizaje al aparecer en él un montón de elementos que quizás son nuevos para ti. A continuación, se matizan o enfatizan algunos de los conceptos más importantes de cada apartado.

Anotaciones al libro#

Cada bloque que leas en el libro de Jurafsky y Martin estará acompañado de un bloque de anotaciones como el siguiente.

Nota

Es recomendable que estudies estos comentarios después de una primera lectura del capítulo y antes de la segunda lectura.

Apartado 5.1

Se introduce el concepto de producto escalar que será una piedra angular de todo lo que está por venir. Si recuerdas cómo se hacía el producto de matrices (que aparecerá numerosas veces más adelante), observarás que este consiste en una serie de cálculos de productos escalares. El sesgo (bias) es importante en algunos problemas porque permite desplazar las fronteras de decisión como demostraremos más adelante. Observa que no linealidad de la exponenciación de la función sigmoide encoge las diferencias entre los valores de salida de la función según nos alejamos del origen, ya que \(\sigma(2)-\sigma(0) >>> \sigma(4)-\sigma(2)\). Por otro lado, no es necesario que hagas la demostración analítica, pero sí que observes gráficamente que \(1 - \sigma(x) = \sigma(-x)\); esta propiedad nos permitirá simplificar algunas ecuaciones. Finalmente, observa que por ahora la función \(\sigma\) se está aplicando a un escalar, pero más adelante se aplicará a un vector o incluso a un tensor de cualquier número de dimensiones. En este caso, la función se aplica elemento a elemento, es decir, si \(\mathbf{x}\) es un vector, \(\sigma(\mathbf{x}) = [\sigma(x_1), \sigma(x_2), \ldots, \sigma(x_n)]\).

Recuerda, por otro lado, que las diferencias entre una función exponencial y una no exponencial (por ejemplo, cuadrática o lineal) está en el ritmo de crecimiento de la función. En el caso de una exponencial como \(f(x)=2^x\), si duplicamos el valor de la entrada, el valor de la salida se eleva al cuadrado: \(f(2x) = 2^{2x} = {(2^x)}^2\). En el caso de una función cuadrática como \(g(x)=x^2\), si duplicamos el valor de la entrada, el valor de la salida se multiplica por 4: \(g(2x)=(2x)^2 = 4x^2\). En el caso de una función lineal como \(h(x)=x\), si duplicamos el valor de la entrada, el valor de la salida también se duplica: \(h(2x)=2x\).

Apartado 5.2

El ejemplo de clasificación de sentimiento de esta sección es interesante porque muestra la técnica usada hasta hace unos años para esta tarea. Se supone aquí que una persona experta en el dominio ha definido las características (features) que ella considera que pueden ser importantes para decidir si una frase tiene connotaciones positivas o negativas. Estas características se calcularán para cada frase mediante otro programa antes de poder pasarlas por el regresor. Este es un proceso costoso, porque requiere expertos de cada dominio y porque el criterio de lo que es relevante o no puede ser subjetivo. El número de características en este caso solía estar alrededor de unas pocas decenas. En la actualidad, los modelos neuronales, como veremos, procesan los datos en bruto y aprenden las características más relevantes (en cantidades de cientos o miles de ellas), aunque en la mayoría de las ocasiones estas no tienen una interpretación lógica para los expertos.

Por otra parte, la idea de normalización puede parecer ahora poco relevante, pero jugará un papel importante en el modelo del transformer para evitar que ciertos valores intermedios se hagan demasiado grandes o pequeños. Si miras la gráfica de la función sigmoide en el apartado anterior, verás que para valores de \(x\) muy grandes o muy pequeños no hay apenas diferencias en el valor de \(\sigma(x)\), por lo que la función no será sensible a pequeños cambios en el valor de \(x\). Además, en estas zonas la función es prácticamente plana, por lo que su derivada es muy pequeña lo que, como veremos más adelante, dificulta el entrenamiento.

Por último, la idea de procesar varios datos de entrada a la vez es también muy importante, ya que permite reducir el tiempo de procesamiento. Puedes ver cómo empaquetando por filas una serie de vectores de entrada y con una simple multiplicación matricial seguida de la aplicación de la función sigmoide se obtiene el resultado de la clasificación de todos los vectores de entrada a la vez. Las GPUs están especializadas en poder realizar estas operaciones matriciales de forma muy eficiente, por lo que siempre intentaremos empaquetar los datos en los denominados mini-batches (mini-lotes, en español) para llenar la memoria de la GPU con la mayor cantidad de ellos y poder procesarlos en paralelo.

Para que la operación de suma del sesgo sea consistente en tamaños, es necesario estirar el sesgo para obtener un vector \(b\) con el mismo tamaño que el número de muestras procesadas a la vez. Cuando trabajemos con PyTorch, veremos que esta operación se realiza automáticamente y que, gracias al mecanismo de broadcasting, no es necesario obtener explícitamente un vector con el valor del sesgo repetido varias veces y podremos sumar directamente el escalar o un tensor unidimensional de tamaño 1.

Apartado 5.3

La función softmax es el equivalente de la función sigmoide cuando se tiene que clasificar una muestra en más de dos clases. En este caso, la función recibe un vector de valores no normalizados (es decir, sin un rango concreto) y lo transforma en un vector de probabilidades de pertenencia a cada una de las clases. Al vector no normalizado se le denomina logits (logit es la función inversa de la función sigmoide). Observa que no podríamos haber normalizado los valores entre 0 y 1 dividiendo cada uno por la suma de todos ellos, porque hay valores negativos que anularían otros positivos. Podríamos haber considerado elevar cada valor del vector de entrada al cuadrado y dividirlo por la suma de todos los cuadrados, pero la función softmax destaca más las diferencias, como hemos comentado, y penaliza más los valores más alejados del máximo:

z = torch.tensor([0.6, 1.1, -1.5 ,1.2, 3.2, -1.1])
squared = z*z / sum(z*z)
softmax= torch.nn.functional.softmax(z, dim=-1)
print(z, squared, softmax)  
# z =       [0.6000, 1.1000, -1.5000, 1.2000, 3.2000, -1.1000]
# squared = [0.0215, 0.0724,  0.1346, 0.0862, 0.6128,  0.0724]
# softmax = [0.0548, 0.0904,  0.0067, 0.0999, 0.7382,  0.0100]

Observa que cuando en este apartado hacemos \(\hat{\mathbf{y}} = \mathrm{softmax} (\mathbf{W} \mathbf{x} + \mathbf{b})\), el vector \(\mathbf{x}\) corresponde a una única muestra, pero, a diferencia de apartados anteriores, \(\mathbf{W}\) es una matriz y \(\mathbf{b}\) es un vector con valores no necesariamente repetidos. En este caso, la matriz \(\mathbf{W}\) de forma \(K \times f\) transforma un vector columna de características de tamaño \(f\) (realmente, \(f \times 1\)) en un vector de logits de tamaño \(K\), donde \(K\) es el número de clases. Si cambiamos la forma de la matriz a \(f \times K\), entonces una operación equivalente se realizaría con \(\hat{\mathbf{y}} = \mathrm{softmax} (\mathbf{x} \mathbf{W} + \mathbf{b})\), donde ahora \(\mathbf{x}\) y \(\mathbf{b}\) son vectores fila (\(1 \times f\)) y no columna.

Observa, asimismo, que en lugar de aplicar la operación a una única muestra (por ejemplo, las características de una sola frase), podemos hacerlo a un lote de estas, apilándolas por filas en una matriz \(\mathbf{X}\) y haciendo \(\hat{\mathbf{y}} = \mathrm{softmax} (\mathbf{X} \mathbf{W} + \mathbf{B})\) o apilándolas por columnas y haciendo \(\hat{\mathbf{y}} = \mathrm{softmax} (\mathbf{W} \mathbf{X} + \mathbf{B})\). En ambos casos, la matriz \(\mathbf{B}\) contendrá repetido \(m\) veces el vector de sesgos \(\mathbf{b}\). El resultado será un lote de \(m\) vectores de logits de tamaño \(K\), uno por cada muestra del lote.

Cuando de ahora en adelante veas una ecuación de una parte de un modelo neuronal en la que se multiplica un lote de vectores por una matriz, puedes identificar que se trata de una transformación lineal que convierte cada uno de los vectores de entrada en otro vector normalmente de tamaño diferente. Recuerda bien esto cuando estudiemos el tema de las redes neuronales hacia adelante.

En este apartado se introduce también el concepto de vector one hot (un vector donde todos los elementos son cero, excepto uno de ellos que vale uno), que usaremos con frecuencia para referirnos al vector con el que compararemos la salida de la red neuronal. Por ejemplo, si tenemos un problema de clasificación de imágenes de dígitos, el vector one hot que correspondería a la etiqueta del 3 sería \(\mathbf{y} = [0,0,0,1,0,0,0,0,0,0]\).

Apartado 5.4

Se avisa de que los dos próximos apartados se centran en la entropía cruzada y el descenso por gradiente para el caso de la regresión logística binaria y que después se retomará la regresión softmax.

Apartado 5.5

La ecuación \(p(y \vert x) = \hat{y}^y (1−\hat{y})^{1-y}\) es solo una forma compacta de escribir matemáticamente la idea de que si tenemos un dato correctamente etiquetado como \(y\) (donde \(y\) es cero o uno), la verosimilitud que el modelo da a este dato es \(\hat{y}\), si el dato está etiquetado como 1 y \(1−\hat{y}\) si está etiquetado como 0. Verosimilitud y probabilidad denotan algo muy similar a efectos prácticos, pero usaremos el término verosimilitud para referirnos a la probabilidad de una serie de datos cuando vamos asignando distintos valores a los parámetros (o pesos) del modelo; por otro lado, si los parámetros no son una variable aleatoria, sino que tienen un valor concreto, hablaremos de la probabilidad que tienen los datos dados los parámetros del modelo.

Un aspecto básico del entrenamiento de redes neuronales es el principio de estimación por máxima verosimilitud. La explicación del capítulo sobre este método puede complementarse con este breve tutorial. La idea básica es ir probando con diferentes valores de los parámetros intentando encontrar los que maximizan la verosimilitud de los datos. En el caso de la regresión logística, esto se traduce en encontrar los valores de los pesos \(\mathbf{w}\) (o bien \(\mathbf{W}\) en el caso de la regresión multinomial) y del sesgo \(b\) (o los sesgos \(\mathbf{b}\)) que maximizan la probabilidad de que los datos etiquetados como 1 tengan una verosimilitud alta de ser 1 y los datos etiquetados como 0 tengan una verosimilitud baja de ser 1.

Aunque en algún momento del capítulo se calcula el valor concreto de la función de pérdida \(L_{CE}(\hat{y},y)\) para un par de datos concretos, nuestro principal interés estará en la forma analítica de la ecuación (5.23), ya que, como se ve en el siguiente apartado, es la que usaremos para calcular el gradiente de la función de pérdida con respecto a los parámetros del modelo y, por tanto, para actualizarlos en cada paso de entrenamiento. No obstante, la media de la función de error sobre un conjunto de datos (bien los datos de entrenamiento, bien los de validación) en forma de un número concreto (0.564, por ejemplo) nos será útil durante el entrenamiento para comprobar si el modelo está mejorando o no sus predicciones sobre el conjunto de entrenamiento.

Aunque pueda parecer contraintuitivo, con el entrenamiento no buscamos que el valor de la entropía cruzada sobre los datos de entrenamiento llegue a cero. Valores muy bajos de la función de error son un signo de lo que se conoce como sobreaprendizaje (overfitting), que suele implicar que cuando el sistema es evaluado sobre datos nuevos, no es capaz de generalizar bien. Para evitarlo, nos guardaremos habitualmente una parte de los datos para evaluar el modelo sobre ellos y comprobar si hay una mejora sobre datos independientes. A este conjunto reducido de datos se le conoce como conjunto de validación (validation set o development set). Cada cierto número de pasos de entrenamiento, el modelo se evaluará sobre el conjunto de validación y se comprobará si el valor de la entropía cruzada sobre este conjunto ha mejorado o no. Si no ha mejorado, se parará el entrenamiento y se usará el modelo que mejor se haya comportado sobre el conjunto de validación. Normalmente, se usa un término de paciencia (patience) que regula el número de pasos de entrenamiento que se avanza sin que el modelo mejore sobre el conjunto de validación antes de detener el entrenamiento. A la hora de evaluar el desempeño sobre el conjunto de validación, no estamos obligados a usar la entropía cruzada, sino que podemos usar cualquier otra función de pérdida que nos interese. Así, si estamos resolviendo un problema de clasificación de imágenes, podemos usar la precisión (accuracy) como medida de desempeño. Además de los conjuntos de datos anteriores (para entrenamiento y validación), también se suele usar un conjunto de datos de prueba (test set) para evaluar el modelo final sobre datos que no han sido vistos por el modelo durante su entrenamiento.

La discusión sobre la entropía cruzada (cross-entropy) se puede extender un poco para ver de dónde viene esta función y por qué minimizarla es equivalente a maximizar la verosimilitud. Más abajo tienes una pequeña explicación de este tema.

Los logaritmos van a aparecer con cierta frecuencia en tu aprendizaje sobre redes neuronales, por lo que es conveniente recordar algunas de sus propiedades:

Logaritmo del producto: \(\log(xy) = \log(x) + \log(y)\)
Logaritmo de la división: \(\log(x/y) = \log(x) - \log(y)\)
Logaritmo de la exponenciación: \(\log(x^a) = a\log(x)\), donde \(a\) es una constante
Logaritmo de uno: \(\log(1) = 0\)

En particular, el logaritmo de un valor entre cero y uno es negativo, por lo que verás que cuando se hable del logaritmo de la probabilidad de un dato (a veces se denota por logprob), este tendrá valores como -4,321 o -12,678. Una probabilidad (logarítmica) de -4,321 es mayor que una de -12,678 y representará, por tanto, un evento más probable.

Apartado 5.6

Para recordar fácilmente cómo afecta la derivada a la actualización de los pesos considera, para simplificar, que la función de error adopta la forma \(x^2\) y observa en la siguiente gráfica cómo cuando el gradiente es negativo (en el punto con la marca de la estrella) es necesario incrementar el peso para reducir el error, mientras que cuando el gradiente es positivo (en el punto con la marca del círculo) es necesario reducir el peso para reducir el error. En la gráfica se muestra también la derivada de la función de error, que es \(2x\).

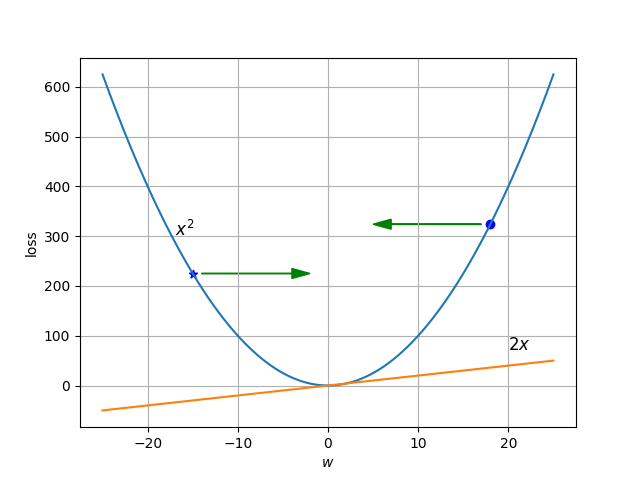
La gráfica anterior ha sido generada con el siguiente código en Python que usa la librería Matplotlib. Estudia qué hace cada instrucción del programa.

import matplotlib.pyplot as plt
import numpy as np
squares = lambda x: x*x
derivative = lambda x: 2*x
x = np.linspace(-25, 25, 500)
y = np.array([squares(xi) for xi in x])
plt.plot(x, y)
plt.text(-17, 300, r'$x^2$', fontsize=12)
plt.scatter(-15, squares(-15), marker="*", color="blue")
plt.arrow(-14, squares(15), 10, 0, head_width=20, head_length=2, width=1, color="green")
plt.scatter(18, squares(18), marker="o", color="blue")
plt.arrow(17, squares(18), -10, 0, head_width=20, head_length=2, width=1, color="green")
y = np.array([derivative(xi) for xi in x])
plt.plot(x, y)
plt.text(20, 72, r'$2x$', fontsize=12)
plt.xlabel(r'$w$')
plt.ylabel('loss')
plt.grid()
plt.savefig("derivativex2.png")

Apartado 5.7

Puedes saltar este apartado sobre la regularización, ya que no es fundamental en estos momentos para entender el funcionamiento básico de las redes neuronales.

Apartado 5.8

Cuando se usa la entropía cruzada como función de error en la regresión multinomial, su forma es muy sencilla, ya que es igual al logaritmo de la probabilidad emitida por el modelo para la clase correcta. No obstante, la complejidad de la derivada dependerá de la complejidad de todo el modelo subyacente. La entropía cruzada es en este caso:

\[L_{CE}(\hat{y},y) = -\log(\hat{y}_i)\]

donde \(\hat{y}_i\) es la probabilidad de que la entrada pertenezca a la clase \(i\), esto es, a la clase correcta. Observa que no se están ignorando las probabilidades de las otras clases, ya que intentar maximizar la probabilidad de la clase correcta implica minimizar la probabilidad de las otras clases.

En el caso de la regresión logística binaria, la función de error es la entropía cruzada binaria, que ya vimos que adopta la siguiente forma:

\[L_{CE}(\hat{y},y) = -y\log(\hat{y}) - (1-y)\log(1-\hat{y})\]

Apartado 5.9

Puedes saltar este apartado.

Apartado 5.10

Se calcula aquí paso a paso el gradiente de la entropía cruzada binaria respecto a cada uno de los parámetros (pesos y sesgo) del regresor logístico binario. Estas son las reglas de derivación que se necesitan para derivar la mayor parte de las funciones de error que se usan en redes neuronales:

Derivada con un exponente: \(\frac{d}{dx}(x^a) = a x^{a-1}\), donde \(a\) es una constante
Derivada con el producto de una constante: \(\frac{d}{dx}(cx) = c\), donde \(c\) es una constante
Derivada de una constante: \(\frac{d}{dx}(c) = 0\)
Derivada de la suma: \(\frac{d}{dx}(x+y) = \frac{d}{dx}(x) + \frac{d}{dx}(y)\)
Derivada del logaritmo: \(\frac{d}{dx}(\log(x)) = \frac{1}{x}\)
Derivada del producto: \(\frac{d}{dx}(xy) = y\frac{d}{dx}(x) + x\frac{d}{dx}(y)\)

Dado que la función de error será una función compuesta de múltiples funciones, la regla de la cadena nos será de suma utilidad:

\[ \displaystyle \frac{\displaystyle d f(g(x))}{\displaystyle dx} = f'(g(x))\cdot g'(x) = \frac{\displaystyle d f}{\displaystyle dg}\cdot \frac{\displaystyle d g}{\displaystyle dx} \]

donde \(f'\) y \(g'\) representan las derivadas de \(f\) y \(g\) respectivamente. Por ejemplo, si \(f(x) = x^2\) y \(g(x) = 2x\), entonces \(f(g(x)) = (2x)^2 = 4x^2\) y aplicando la regla de la cadena:

\[ \displaystyle \frac{\displaystyle d f(g(x))}{\displaystyle dx} = f'(g(x))\cdot g'(x) = \frac{\displaystyle d ((2x)^2)}{\displaystyle d 2x}\cdot \frac{\displaystyle d 2x}{\displaystyle dx} = 4x\cdot 2 = 8x \]

Sería interesante que calcularas la derivada de la entropía cruzada binaria respecto al umbral (en el libro se muestra la derivada respecto a los pesos) y que te animaras a calcular también el gradiente para el caso de la regresión logística multinomial.

Entropía#

Considera el caso en que el que un suceso \(x\) puede ocurrir con una probabilidad \(p_x\) modelada mediante una determinada distribución de probabilidad \(p\). Supongamos que queremos calcular la cantidad de información \(I(x)\) de dicho suceso o, en palabras más sencillas, la sorpresa que nos produciría que este suceso tuviera lugar. Como primera aproximación, es fácil ver que la inversa de la probabilidad, \(1/p_x\), da un valor mayor cuando la probabilidad es pequeña (nos sorprende más que ocurra algo improbable) y un valor menor cuando la probabilidad es mayor (nos sorprende poco que ocurra algo muy probable).

Además, parece lógico que la cantidad de información de un suceso seguro (con probabilidad 1) sea 0. Para conseguirlo, dado que el logaritmo es una función monótona creciente, podemos aplicar el logaritmo al cociente anterior sin que cambie el orden relativo de dos sucesos con diferentes probabilidades:

\[ I(x) = \log\left(\frac{1}{p_x}\right) = - \log (p_x) \]

La cantidad de información se mide en bits si el logaritmo es en base 2 y en nats si es en base \(e\). La entropía \(H\) de la distribución de probabilidad es una medida de la información promedio de todos los posibles sucesos. Para obtenerla basta con ponderar la información de cada suceso por su probabilidad y sumar sobre todos los sucesos:

\[ H(p) = - \sum_{x} p_x \log(p_x) \]

Comprueba que la entropía es máxima si todos los sucesos son equiprobables. La entropía cruzada entre dos distribuciones de probabilidad mide la sorpresa que nos provoca un determinado suceso si usamos una distribución de probabilidad \(q\) alternativa a la probabilidad real \(p\):

\[ H(p,q) = - \sum_{x} p_x \log(q_x) \]

Puedes ver, por lo tanto, que la fórmula (5.21) del libro coincide con la ecuación anterior: maximizar la verosimilitud respecto a los parámetros del modelo es equivalente a minimizar la entropía cruzada \(H(y,\hat{y})\).