




Next: DTRNN behaving as finite-state
Up: Languages, grammars and automata
Previous: Grammars
Contents
Index
Chomsky's hierarchy of grammars
Grammars are usually classified according to a hierarchy established by
Chomsky (1965) (see also (Hopcroft and Ullman, 1979) or
Salomaa (1973, 15)), according to the form of
their productions. Each of the levels in the hierarchy has a corresponding
automaton class:
- Type 0 or unrestricted (all possible
grammars). Languages generated are recognized by Turing machines (automata that read from
and write on an endless tape, which will be defined in
section 4.3.1). Recognizing a
string is outputting ``yes''
if the string belongs to the language.
- Type 1 or context-sensitive:
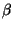 never
shorter than
never
shorter than 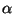 ,
,
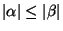 (except for
(except for
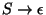 ). Languages generated are recognized
by linearly-bounded automata (a subclass of Turing machines, see
section 4.3.1).
). Languages generated are recognized
by linearly-bounded automata (a subclass of Turing machines, see
section 4.3.1).
- Type 2 or context-free:
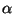 is a single variable (
is a single variable (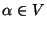 ). The class
of languages generated by type 2 grammars is exactly the class of
languages recognized by pushdown
automata (PDA,
Hopcroft and Ullman (1979, 110), Salomaa (1973, 34)), which
may be seen as finite-state
machine
which can push symbols into and pop symbols from
an infinite stack. A
(nondeterministic) pushdown automaton is a 7-tuple
). The class
of languages generated by type 2 grammars is exactly the class of
languages recognized by pushdown
automata (PDA,
Hopcroft and Ullman (1979, 110), Salomaa (1973, 34)), which
may be seen as finite-state
machine
which can push symbols into and pop symbols from
an infinite stack. A
(nondeterministic) pushdown automaton is a 7-tuple
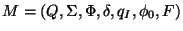 where:
where:
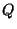 is the finite set of states, with
is the finite set of states, with 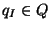 the initial state;
the initial state;
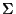 is the finite input alphabet;
is the finite input alphabet;
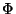 is a finite set of symbols which may be
stored in the stack, which is not initially empty, but instead
contains a special symbol
is a finite set of symbols which may be
stored in the stack, which is not initially empty, but instead
contains a special symbol 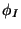 ;
;
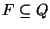 is the subset of accepting
states.
is the subset of accepting
states.
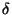 is the next-state or transition
function
of the automaton, which maps
is the next-state or transition
function
of the automaton, which maps
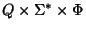 into finite
subsets of
into finite
subsets of
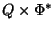 ; that is, when the
PDA is in a state, reads in a
string, pops a symbol from the stack, changes state, and pushes zero or more symbols into the
stack, nondeterministically choosing the next state and the symbols
pushed from a finite set of choices.
; that is, when the
PDA is in a state, reads in a
string, pops a symbol from the stack, changes state, and pushes zero or more symbols into the
stack, nondeterministically choosing the next state and the symbols
pushed from a finite set of choices.
The PDA is said to accept an input string from 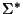 when it is
led to at least one accepting state in
when it is
led to at least one accepting state in 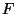 . An alternate acceptance
criterion prescribes an empty stack at the end of the processing.
. An alternate acceptance
criterion prescribes an empty stack at the end of the processing.
- Type 3 or regular:
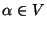 ,
, 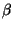 contains
at most one variable at the right end.
Languages generated are recognized by deterministic finite-state
automata (see section 2.3.3).
contains
at most one variable at the right end.
Languages generated are recognized by deterministic finite-state
automata (see section 2.3.3).





Next: DTRNN behaving as finite-state
Up: Languages, grammars and automata
Previous: Grammars
Contents
Index
Debian User
2002-01-21
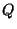 is the finite set of states, with
is the finite set of states, with 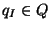 the initial state;
the initial state;
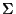 is the finite input alphabet;
is the finite input alphabet;
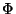 is a finite set of symbols which may be
stored in the stack, which is not initially empty, but instead
contains a special symbol
is a finite set of symbols which may be
stored in the stack, which is not initially empty, but instead
contains a special symbol 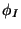 ;
;
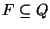 is the subset of accepting
states.
is the subset of accepting
states.
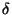 is the next-state or transition
function
of the automaton, which maps
is the next-state or transition
function
of the automaton, which maps
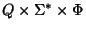 into finite
subsets of
into finite
subsets of
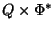 ; that is, when the
PDA is in a state, reads in a
string, pops a symbol from the stack, changes state, and pushes zero or more symbols into the
stack, nondeterministically choosing the next state and the symbols
pushed from a finite set of choices.
; that is, when the
PDA is in a state, reads in a
string, pops a symbol from the stack, changes state, and pushes zero or more symbols into the
stack, nondeterministically choosing the next state and the symbols
pushed from a finite set of choices.