- ...Motivation1.1
- A slightly edited version of the original preface
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... trained2.1
- Of course, in reasonable time, as Marvin Minsky
remarks in his foreword to the book by
Siu et al. (1995).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... S.C.3.1
- Available as a PDF file at
http://www.dlsi.ua.es/~mlf/nnafmc/papers/kleene56representation.pdf,
retyped by Juan Antonio Pérez-Ortiz
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
.3.2
- Some of these architectures
use sigmoid units whose output is
real and continuous instead of TLU whose output is discrete; for
details, see section 3.2.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
measured.4.1
- Other authors (Stiles and Ghosh, 1997; Stiles et al., 1997) prefer
to see sequences as functions that take an integer and return a
value in
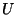 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... classes:4.2
- This classification
is inspired in the one given by Hertz et al. (1991, 177).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... DTRNN,4.3
- Defined in
section 3.2.1.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...state!units;4.4
- All state units are assumed to be of the same kind.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
![${\bf u}[t]$](img135.png) 4.5
4.5
- Unlike in
eqs. (3.1-3.3), bold lettering is used here to emphasize the vectorial nature of
states, inputs, outputs, and next-state and output functions.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... network!second-order4.6
- Second-order neural
networks operate on products of two inputs, each input taken
from a different subset; first-order
networks instead, operate on raw inputs.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... function4.7
- Also called transfer function,
gain function and squashing function (Hertz et al., 1991, 4).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...clouse94t)4.8
- The class of
finite-state recognizers representable in TDNN is that of definite-memory machines
(DMM), that is, finite-state machines whose state is observable
because it may be determined by inspecting a finite window of past
inputs (Kohavi, 1978). When the state is observable but has to be
determined by inspecting both a finite window of past
inputs and a finite window of past
outputs, we have a finite-memory machine
(FMM); the neural equivalent of FMM is
therefore the NARX network just mentioned.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... perform4.9
- Although
the choice of a particular encoding scheme or a particular kind of
preprocessing --such as e.g. a normalization-- may indeed affect
the performance of the network.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... parameter4.10
- Learning the initial state is surprisingly not
too common in DTRNN literature, because it seems rather
straightforward to do so; we may cite the papers by
Bulsari and Saxén (1995) Forcada and Carrasco (1995), and
Blair and Pollack (1997).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
once.4.11
- For a detailed discussion of gradient-based learning
algorithms for DTRNN and their modes of application, the reader is
referred to an excellent survey by Williams and Zipser (1995), whose emphasis
is on continuously running DTRNN.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
zero.4.12
- Derivatives with respect to the components of the
initial state
![${\bf x}[0]$](img219.png) may also be easily computed
(Forcada and Carrasco, 1995; Bulsari and Saxén, 1995; Blair and Pollack, 1997), by initializing them accordingly (that is,
may also be easily computed
(Forcada and Carrasco, 1995; Bulsari and Saxén, 1995; Blair and Pollack, 1997), by initializing them accordingly (that is,
![$\partial
x_i[0]/\partial x_j[0]=\delta_{ij}$](img220.png) ).
).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... valence.4.13
- The valence
(also arity) of a tree is the
maximum number of daughters that can be found in any of its nodes.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
daughters)4.14
- Stolcke and Wu (1992) added a special
unit to the state pattern which is
an indicator showing whether the pattern is a terminal
representation.
Another possibility would be to add a special output neuron.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- .... 5.1
- Here, an abbreviated
notation for the concatenation of
languages,
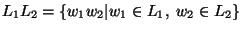 , is used.
, is used.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...symbol!useless).5.2
- This occurs also when a
string containing the variable may be derived in more than one step
from another string containing it, that is, when recursion is
indirect.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... DTRNN.5.3
- As usual,
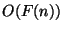 ,
with
,
with
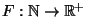 , denotes the set of all
functions
, denotes the set of all
functions
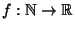 such that, for any
such that, for any
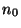 there exists a positive constant
there exists a positive constant 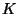 such that, for all
such that, for all
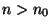 ,
, 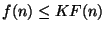 (upper bound). Similarly, a lower bound may
be defined;
(upper bound). Similarly, a lower bound may
be defined; 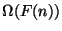 denotes the set of all functions
denotes the set of all functions
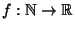 such that, for any
such that, for any 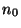 there
exists a positive constant
there
exists a positive constant 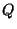 such that, for all
such that, for all 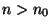 ,
,
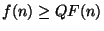 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... states,5.4
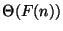 , with
, with
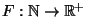 , is the set of all functions
, is the set of all functions
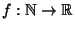 belonging both to
belonging both to 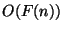 and
and
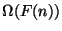 (see the preceding footnote).
(see the preceding footnote).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... nondenumerable5.5
- A set is denumerable (also countable) when
there is a way to assign a unique natural number to each of the
members of the set. Some infinite sets are nondenumerable (or uncountable); for example, real numbers form a nondenumerable
set.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
0).5.6
- In the same spirit,
Carrasco et al. (2000) have recently proposed
similar encodings for general Mealy and Moore machines on various first- and second-order
DTRNN architectures.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
nondeterministic5.7
- Nondeterminism does not add any power to
Turing machines.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...salomaa73b)5.8
- These machines are called
linearly-bounded automata because a deterministic
TM having its tape
bounded by an amount which is a linear function of the length of the
input would have the same computational power as them.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
computation5.9
- Nonuniform TMs are
unrealizable because the length of
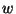 is not bounded, and thus, the
number of possible advice strings is infinite and cannot be stored
in finite memory previous to any computation.
is not bounded, and thus, the
number of possible advice strings is infinite and cannot be stored
in finite memory previous to any computation.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... task)6.1
- For some recognition
tasks, positive samples may be enough.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 0.36.2
- This is
presumably because in each state, and for the language studied by
Cleeremans et al. (1989), there is a maximum of two possible successors,
and 0.3 is a safe threshold below 0.5.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...parsing!shift-reduce.6.3
- Also known as LR, Left-to-right, Rightmost-derivation parsing (Hopcroft and Ullman, 1979, 248).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.