TEMA 3: Tipos Abstractos de Datos: Árboles, Grafos.
Contenidos
1. Árboles
- Es un TAD que representa una colección de elementos llamados nodos.
- Uno de estos nodos es especial, nos referimos a él como la raíz del árbol.
- Entre los nodos hay una relación de paternidad la cual impone una estructura jerárquica sobre ellos.
1.1. Definición
- El TAD Árbol se suele definir de manera recursiva:
- Un sólo nodo es por sí mismo un árbol. Este nodo es la raíz del árbol.
- Dado un nodo \(n\) y una serie de árboles \(A_1, A_2, ... , A_k\) con raíces \(n_1, n_2, ..., n_k\), podemos crear un nuevo árbol haciendo que \(n\) sea el padre de los nodos \(n_1, n_2, ..., n_k\). Decimos entonces que \(n\) es la raíz del nuevo árbol, \(A_1, ..., A_k\) son subárboles de la raíz y a los nodos \(n_1, n_2, ..., n_k\) son hijos del nodo \(n\).
- Un árbol vacío se representa por la letra griega \(\Lambda\).
- Los TADs
Árbolse emplean p.e. en lugar deListascuando la cantidad de elementos almacenada es muy grande y el tiempo de acceso lineal es costoso.
1.2. Aspecto
Se suelen representar de este modo
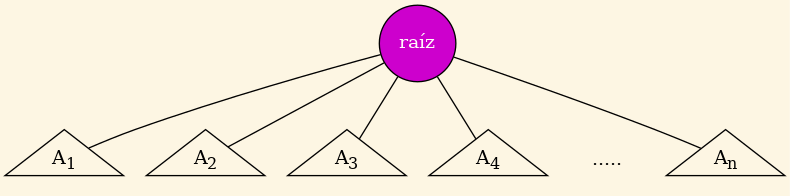
Figure 1: Ejemplo general.
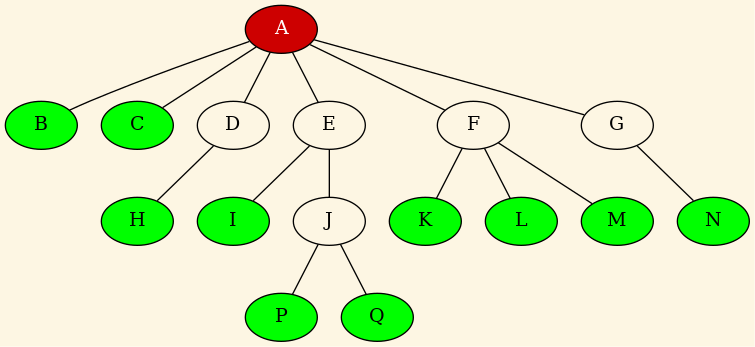
Figure 2: Un árbol concreto.
1.3. Conceptos
- Si
res la raíz de unÁrbolse dice que cada subárbol es un hijo dery queres el padre de la raíz de cada uno de los subárboles. - En un
Árbolcon \(n\) nodos hay \(n-1\) aristas. - En principio cada nodo puede tener un número arbitrario de hijos, incluso \(0\).
- Los nodos sin hijos se llaman hojas.
- Los nodos con el mismo padre son hermanos.
- Un camino de un nodo \(n_1\) a otro \(n_k\) se define como la secuencia de nodos \(n_1, n_2, ..., n_k\) tal que \(n_i\) es el padre de \(n_{i+1}\) , \(\forall i : 1 \le i < k\). Su longitud es el número de aristas que lo forman, \(k-1\).
- Existe un camino de longitud cero entre cada nodo y él mismo.
- En un
Árbolhay sólo un camino de la raíz a cada nodo.
- Para un nodo \(n_i\) su profundidad es la longitud del camino único desde la raíz a ese nodo. Luego la profundidad de la raíz es \(0\).
- La altura de \(n_i\) es el camino más largo desde \(n_i\) a una
hoja. Luego la altura de cualquier hoja es \(0\), y la altura de un
Árboles la altura de su raíz. - La profundidad de un
Árboles la profundidad de la hoja más profunda, es decir, su altura.
- Si \(n_1 \ne n_2\) se dice que \(n_1\) es un antecesor propio de \(n_2\), y que \(n_2\) es un descendiente propio de \(n_1\).
- Los
Árbolescuyos nodos pueden tenernhijos se denominan n-arios. El caso particular en el cual ningún nodo tiene más de dos hijos se denominaÁrbol binario. - Si hay un camino de \(n_1\) a \(n_2\) se dice que \(n_2\) es descendiente de \(n_1\) y a su vez \(n_1\) es el antecesor de \(n_2\).
1.4. Orden de los nodos
- Los hijos de un nodo pueden estar ordenados o no.
- Caso de estarlo, se suele hacer de izquierda a derecha.
- Si no se ordenan por ningún criterio el
Árbolse llama no ordenado.
- La ordenación es útil en el caso de dos nodos cualesquiera entre
los cuales no existe relación antecesor/descendiente. Entonces si
aybson hermanos yaestá a la izquierda deb, entonces todos los descencientes deaestán a la izquierda deby de todos sus descendientes.
1.5. Recorrido ordenado de un Árbol
- Tenemos varias formas de recorrer ordenadamente un
Árbol. - Pre-orden -orden previo- , In-orden -orden simétrico- y Post-orden -orden posterior-.
- Estos ordenamientos se definen recursivamente así:
- Si un
ÁrbolA es nulo, entonces la lista vacía es el listado de los nodos de A en los órdenes previo, simétrico y posterior. - Si A contiene un solo nodo, este único nodo es el listado de los nodos de A en los órdenes previo, simétrico y posterior.
- Pero si ninguno de los anteriores es el caso…
- Si un
Sea A un Árbol con raíz \(n\) y subárboles \(A_1, A_2,...,A_k\)
representado de este modo:
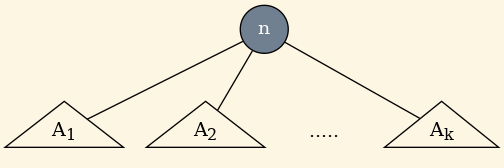
Entonces…
- El listado en orden previo de los nodos de A está formado por la raíz de A, seguida de los nodos de \(A_1\) en orden previo, luego por los nodos de \(A_2\) en orden previo y así sucesivamente hasta los nodos de \(A_k\) en orden previo.
- El listado en orden simétrico de los nodos de A está formado los nodos de \(A_1\) en orden simétrico, seguidos de \(n\), y detrás los nodos de \(A_2, ..., A_k\) con cada grupo de nodos en orden simétrico.
- El listado en orden posterior de los nodos de A tiene los nodos de \(A_1\) en orden posterior, luego los de \(A_2\) en orden posterior y así sucesivamente hasta los de \(A_k\) en orden posterior y por último la raíz \(n\).
2. Árboles. Operaciones básicas
- Parent (n) : Devuelve el padre del nodo
n. Sines la raíz (no tiene padre) se devuelve \(\Lambda\). En este caso podemos interpretar \(\Lambda\) como un nodo nulo que indica que se ha salido del árbol. - LeftMostChild (n) : Devuelve el hijo más a la izquierda del nodo
no \(\Lambda\) sines una hoja (no tiene hijos).
- RightSibling (n) : Devuelve el hermano a la derecha del nodo
n, el cual se define como el nodomque tiene el mismo padrepquen, de manera quemestá inmediatamente a la derecha denen el ordenamiento de los hijos dep. Fíjate que también puede devolver \(\Lambda\) si es el caso.
- Label (n) : Devuelve la etiqueta del nodo
n. - Create (v, \(A_1, A_2, ..., A_i\)) : Crea y devuelve un nuevo nodo
rque tiene etiquetavy le asigna \(i\) hijos que son las raíces de los árboles \(A_1, A_2, ..., A_i\), en ese orden desde la izquierda. Si \(i = 0\) entoncesres la raíz y una hoja.
- Root () : Devuelve la raíz del árbol o \(\Lambda\) si el árbol es nulo.
- MakeNull () : Convierte el árbol en nulo.
- Search (x) : Devuelve el nodo que contiene el dato
xo null si el dato no está en el árbol. - Insert (x) : Inserta en el lugar que le corresponde un nodo con
dato = x.
- Delete (x) : Elimina el nodo con
dato = x.
Posibilidades:- Si es un nodo hoja, se puede eliminar directamente.
- Si el nodo solo tiene un hijo, este hijo pasa a ser hijo de su abuelo.
Vamos a borrar el nodo 4:
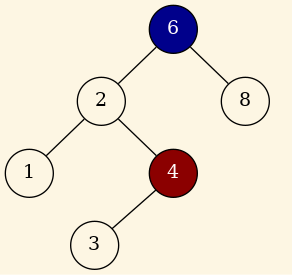
Figure 3: Borrado del nodo 4.
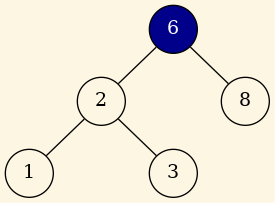
Figure 4: Nodo 4 borrado.
- Si el nodo tiene dos hijos podemos sustituir el dato de este nodo por el dato más pequeño del subárbol derecho y eliminar ese nodo del subarbol derecho.
Vamos a borrar el nodo 2 :
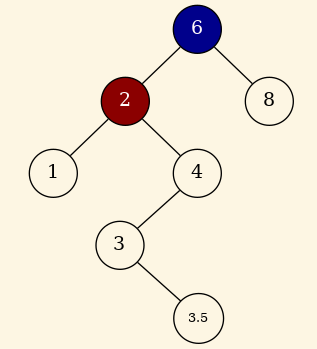
Figure 5: Borrado del nodo 2.
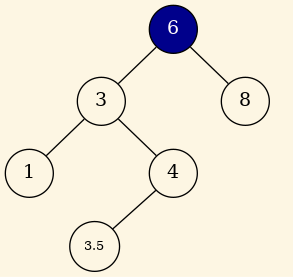
Figure 6: Nodo 2 borrado.
3. Árboles. Implementación
3.1. Mediante vectores
- Necesitamos numerar los nodos del árbol: \(0, 1, 2, ..., n\).
- Creamos un vector \(L\) de enteros donde el índice \(i\) representa al nodo actual y su contenido \(j\) es el índice en el vector de su padre.
- El nodo que representa la raíz tiene asignado el valor \(0\).
- Según esto si \(L[i] = j\), entonces \(j\) es el padre del nodo \(i\) y \(L[i] = 0\) si el nodo \(i\) es hijo de la raíz.
- Esta representación complica la implementación de determinadas operaciones, por lo que emplearemos otra.
3.2. Mediante listas de hijos
- Cada nodo mantiene una lista de sus nodos-hijo.
- Si el número máximo de hijos es fijo, podríamos incluso usar un vector de nodos.
3.3. Clases necesarias para la representación
Necesitamos al menos dos clases de Alto Nivel:
- Tree
typedef char Element; // Hasta que veamos genericidad... class Tree { public: Tree (void) { fRoot = nullptr; } ~Tree (void); void insert (const Element &i); private: NodePtr fRoot; };
Y la otra:
- Node
class Node { public: Node (Element i) { fItem = i; } ~Nodo (void) {} Tree& sibling (int n) { return fSiblings[n]; } Tree& leftSibling (void) { return fSiblings[0]; } Tree& rightSibling (void) { return fSiblings[1]; } Element& item (void) { return fItem; } private: Element fItem; Tree fSiblings[2]; // Como máximo 2 hijos };
3.4. Árboles binarios
- Se trata de un tipo especial de árbol. Algunos de los ejemplos que hemos visto previamente usan este tipo de árboles.
- Un nodo tiene como máximo dos hijos.
- A estos hijos se les llama hijo izquierdo (LeftSibling ) e hijo derecho (RightSibling ).
- A menudo se emplean estableciendo una relación de órden, el dato del hijo izquierdo es menor que el dato de su padre, y el dato del hijo derecho es mayor que el dato del padre.
3.5. Árboles binarios
- Esto permite hacer inserciones automáticas en base a la etiqueta del nodo nuevo insertado.
- Por ejemplo, si insertamos en un arbol binario ordenado de enteros la secuencia de números (\(8, 5, 9, 4, 1, 6, 2\)) obtendríamos el árbol:
Árbol resultado de insertar por este orden: \(8, 5, 9, 4, 1, 6, 2\)
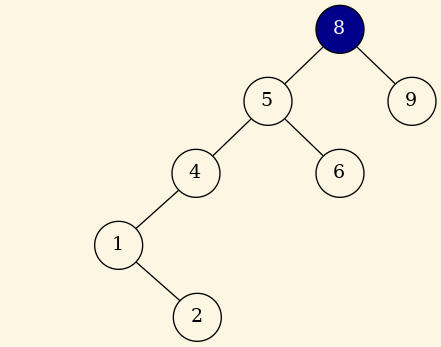
Figure 7: Insertamos 8, 5, 9, 4, 1, 6, 2.
3.6. Árboles de otros tipos.
- Los árboles n-arios o la particularización llamada árbol binario no son los únicos tipos de árboles.
- Es interesante que eches un vistazo a estos otros tipos de árboles y que veas por qué se caracterizan:
4. Grafos
- En problemas de disciplinas como la informática, las matemáticas, diversas ingenierías, etc… a menudo necesitamos representar relaciones (de distinto tipo) entre objetos.
- Estas relaciones podemos plasmarlas mediante el uso de una estructura de datos conocida como Grafo.
- A grandes rasgos un grafo es un conjunto de vértices y uno de aristas que conectan esos vértices.
- Existen grafos de distinto tipo en función de las
características en las que nos fijemos:
- Dirigidos y no dirigidos.
- Etiquetados y no etiquetados (ponderados).
- Aleatorios ( las aristas están asociadas a una probabilidad ).
- Cíclicos y acíclicos.
- etc…
5. Grafos. Definiciones
- Un grafo \(G\) se define como un par \(G = ( V, E )\), donde \(V\) es un conjunto de vértices y \(E\) es un conjunto de aristas.
- Cada arista (o arco ) es, a su vez, un par \(( v, w ) : v,w \in V\). Si este par es ordenado, entonces el grafo es dirigido (digrafo ).
Un vértice \(w\) es adyacente a otro \(v\) \(\iff (v, w) \in E\).
Aclaración : \((p \iff q) \equiv (p \rightarrow q) \wedge (q \rightarrow p)\).
- En un grafo no dirigido la arista \((w, v)\) es equivalente a la \((v, w)\) y por tanto \(w\) es adyacente \(v\) y \(v\) es adyacente a \(w\).
- En un grafo no dirigido se llama grado de un vértice al número de aristas que inciden en el. En un grafo dirigido hablamos de grado de entrada y grado de salida.
- Un camino en un grafo es una secuencia de vértices \(w_1, w_2, ..., w_n : (w_i, w_{i+1}) \in E, \forall\ 1 \le i < n\). Si \(w_1 = w_n\) se habla de camino cerrado.
- La longitud de un camino es el número de aristas del mismo, o lo que es lo mismo \(n-1\). Se pueden permitir caminos de un vértice a sí mismo.
- Una arista \((v, v)\) de un vértice a sí mismo da lugar a un camino llamado ciclo. Por tanto un ciclo es un camino de longitud mínima igual a 1. Un grafo sin ciclos se considera acíclico.
- Se llama grafo conexo o conectado a uno no-dirigido que tiene un camino desde cualquier vértice a cualquier otro. Si el grafo fuera dirigido, entonces se le llama fuertemente conexo.
- Si un grafo dirigido no es fuertemente conexo pero el grafo subyacente no dirigido (sin direccion en las aristas) es conexo, entonces se le llama débilmente conexo.
- Se llama grafo completo a aquel que tiene una arista entre cualquier par de vértices.
6. Grafos. Operaciones básicas
- First (v): Devuelve el índice del primer vértice adyacente a
v. Si no hay ninguno, se devuelve un valor que represente un vértice nulo. - Next (v, i): Devuelve el índice posterior a
ide entre los vértices adyacentes av. Siies el último índice de los vertices adyacentes avse devuelve un valor que represente un vértice nulo. - Vertex (v, i): Devuelve el vértice cuyo índice
iestá entre los vértices adyacentes av.
7. Grafos. Implementación
Usaremos grafos dirigidos, los no dirigidos se pueden representar de manera similar.
7.1. Matriz de adyacencia
- Una primera representación consiste en hacer uso de una matriz de adyacencia.
- Se trata de una matriz bidimensional, llamése \(a\), donde para cada arista \((u,v)\) del grafo hacemos \(a[u][v] = 1\), y si no existe dicha arista \(a[u][v] = 0\).
- Si la arista tiene un peso asociado \(p\) : \(a[u][v] = p\). En estos casos podemos usar un peso muy grande o muy pequeño (\(\infty, -\infty\)) para indicar que una arista no existe.
- Pega: excesivo consumo de memoria. Sin embargo es válida si el grafo es denso: \(\mid A \mid\ \simeq\ {\mid V \mid}^2\).
7.2. Lista de adyacencia
- Si el grafo no es denso (disperso ) se usa una lista de adyacencia.
- Cada vértice mantiene una lista de todos los vértices adyacentes.
- Por lo tanto el espacio necesario de almacenamiento pasa a ser \(\simeq\ \mid A \mid + \mid V \mid\).
- De este modo, una operación muy habitual en grafos como es encontrar todos los vértices adyacentes a uno dado consiste en recorrer la lista de adyacencia del vértice en cuestión.
7.3. Ejemplo
El siguiente grafo:
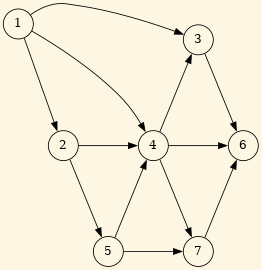
Figure 8: Grafo de partida.
Produce esta lista de adyacencia:
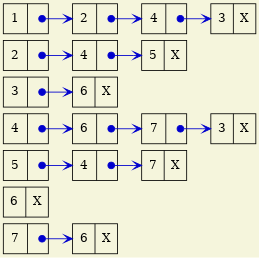
Figure 9: Lista de adyacencia obtenida.
8. Grafos. Tipos de problemas
- Conectividad:
- Consiste en saber decir si un grafo es conexo o no. Se trata de un problema básico ya que la solución a algunos otros problemas dependen de esta respuesta.
- Alcanzabilidad:
- El problema de la alcanzabilidad está relacionado con la conexión. En él se nos dan un grafo \(G(V, E)\), un vértice origen \(s \in V\) y un vértice destino \(d \in V\) y tenemos que decir si existe un camino de \(s\) a \(d\) (\(s \rightsquigarrow d\)).
- Recorrido:
- Consiste en visitar sistemáticamente todos los nodos de un grafo.
- Caminos más cortos:
- Partiendo del caso anterior es posible llegar a \(d\) desde \(s\) por varios caminos. Es posible que nos interese el camino más corto (\(G\) no-dirigido), de menor coste (\(G\) ponderado), etc…
- Hay variantes:
- de un origen \(s\) a un solo destino \(d\).
- de un origen \(s\) a todos los posibles destinos \(d\), uno a uno.
- \(\forall (u, v) \mid u,v \in V\) se nos pide encontrar el camino más corto de \(u\) a \(v\).
- Árboles de expansión:
Consiste en encontrar un árbol de expansión en el grafo. Este se define como: dado un grafo conexo y no-dirigido \(G = (V, E)\), un árbol de expansión es un subconjunto acíclico \(T \subseteq E\) que conecta todos los vértices de \(G\).
Si el grafo es ponderado este problema se transforma en encontrar el árbol de expansión mínima.
- Ordenación topológica:
- Consiste en ordenar los vértices de un grafo dirigido acíclico, de manera que si hay un camino desde \(v_i\) a \(v_j\) entonces \(v_j\) aparece después de \(v_i\) en la ordenación.
9. Grafos. Algoritmos
9.1. Ordenación topologica
Asigna un orden lineal a los vértices de un GDA de manera que si existe una arista de \(i \rightarrow j\), entonces \(i\) aparece antes que \(j\) en el ordenamiento lineal.
Algoritmo:
int[] topologicalOrder (Graph g) { for cont = 0..|V|-1 { v = vertInDegree0(); // Nuevo vertice grado entrada == 0 if (v < 0) error ("ciclo"); else { num_top[v] = cont; // Vertice 'v' ocupa la posicion 'cont' en el orden topologico for w adjacent to v // Eliminamos 'v' del grafo. --inDegree[w]; } } return num_top; }
9.2. Camino más corto en grafo ponderado desde un sólo origen
Algoritmo:1
// Asume que no hay etiquetas negativas asociadas a ninguna arista void Dijkstra(Graph G, vector<Weight>& D) { // Comenzamos en 1 el indice en vectores y matrices S = {1}; // Nodo 1 guardado en conjunto S for i = 2 .. n D[i] = C[1][i]; // Inicializamos D con el coste de ir de 1..i for i = 1 .. n-1 { seleccionamos w en V-S tal que D[w] es un minimo; añadimos w a S; foreach vertex v en V-S D[v] = min(D[v], D[w] + C[w][v]); // C[w][v] == INFTY si no existe w->v } }
Si aplicamos Dijkstra a este grafo:
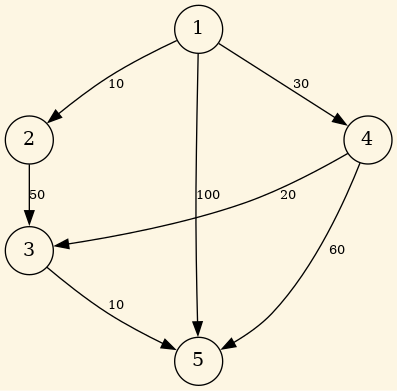
Figure 10: Dijkstra.
| Iteración | S | w | D[2] |
D[3] |
D[4] |
D[5] |
|---|---|---|---|---|---|---|
| Inicial | {1} | - | 10 | \(\infty\) | 30 | 100 |
| 1 | {1,2} | 2 | 10 | 60 | 30 | 100 |
| 2 | {1,2,4} | 4 | 10 | 50 | 30 | 90 |
| 3 | {1,2,4,3} | 3 | 10 | 50 | 30 | 60 |
| 4 | {1,2,4,3,5} | 5 | 10 | 50 | 30 | 60 |
9.3. Árbol de expansión mínima
- Un árbol de expansión de un grafo no dirigido \(G = (V, E)\) es un árbol formado por todos los vértices de \(G\) y algunas de (pueden ser todas) las aristas de \(G\), de manera que no hay ciclos.
- Si cada arista \((u, v)\) \(\in E\) tiene asociado un peso (\(G\) es ponderado), al árbol de expansión cuyas aristas pesan lo mínimo, se le llama arbol de expansión mínima.
9.4. Árbol de expansión mínima. Prim
Algoritmo: La entrada al agoritmo la constituyen el grafo \(G\) y la salida se devuelve en T que es un conjunto de aristas.
void Prim (Graph G, set<Edge>& T) { set<Vertex> U; Vertex u, v; T = {}; U = {1}; while U != V { (u, v) arista con coste mínimo tal que u esta en U y v en V-U; T = T + {(u, v)}; U = U + {v}; } }
- Y aquí encontrarás una explicación de su funcionamiento.
Aplicar Prim al siguiente grafo:
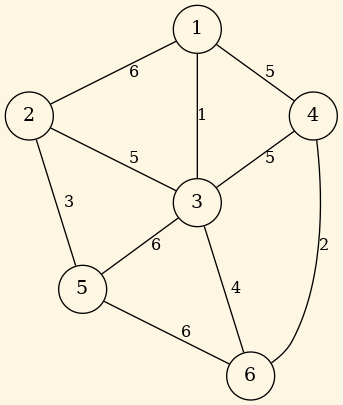
Figure 11: Prim.
Produce en este orden estas aristas: T = { (1,3) , (3,6), (6,4) , (3,2) , (2,5) }
9.5. Árbol de expansión mínima. Kruskal
Algoritmo:
void Kruskal (Graph G, set<Edge>& T) { T = {}; V; // todos los Arcos del grafo G Mientras (T contenga menos de n-1 arcos y V != {}) { De las aristas en E seleccionar la de menor coste (i,j) V = V - {(i,j)}; Si el nodo-i y el nodo-j no están en el mismo árbol entonces T = T + {(i,j)} } }
- Y aquí encontrarás una explicación de su funcionamiento.
Aplicar Kruskal al siguiente grafo:
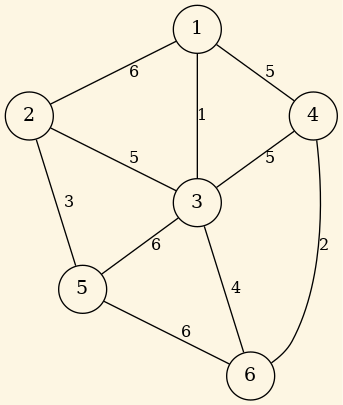
Figure 12: Kruskal.
Produce en este orden estas aristas: T = { (1,3) , (4,6), (2,5) , (3,6) , (3,2) }
9.6. Recorrido. Búsqueda en profundidad
- Vamos a ver el algoritmo de búsqueda en profundidad.
Es una generalización del recorrido en orden previo de un árbol.
bool visited[N]; // N = numero de nodos del grafo for i = 0..N-1 visited[i] = false; for i = 0..N-1 if not visited[i] dfs (i); void dfs (Vertex v) { Vertex w; visited[v] = true; for w in L[v] // Para todo nodo w adyacente a v if not visited[w] dfs (w); }
9.7. Visualización de grafos
- Te puede resultar interesante este software: Graphviz.
- Con él puedes describir mediante un lenguaje formal grafos y otros tipos de información estructural.
- Echa un vistazo a la colección de ejemplos que hay en su página.
- Los grafos y árboles que aparecen en este tema están hechos con Graphviz. La herramienta empleada ha sido dot.
10. Aclaraciones
- En ningún caso estas transparencias son la bibliografía de la asignatura, por lo tanto debes estudiar, aclarar y ampliar los conceptos que en ellas encuentres empleando los enlaces web y bibliografía recomendada que puedes consultar en la página web de la ficha de la asignatura y en la web propia de la asignatura.
Footnotes:
El algoritmo de Floyd-Warshall resuelve de manera más directa el problema de los caminos más cortos entre todos los pares.