TEMA 2: Tipos Abstractos de Datos
Listas, Pilas, Colas.
Programación-II, Universidad de Alicante, 2025-26
Created: 2025-02-04 mar 00:33
Presentación
- Son una serie de TADs considerados fundamentales.
- Las listas son secuencias de elementos.
- Pueden ser implementadas de distinto modo.
- Pilas y colas son un tipo especial de listas
Listas
- Son flexibles, pueden crecer y decrecer.
- Podemos acceder a cualquier posición dentro de la lista.
- Podemos insertar y borrar elementos de cualquier posición.
- Pueden ser concatenadas o divididas (sublistas ).
- Una lista se suele representar como una sucesión de elementos separados por comas: \(a_1, a_2, ..., a_n : n >= 0\).
Listas
- Matemáticamente una lista es una secuencia de cero o más elementos.
- Si tiene \(0\) elementos se llama lista vacía.
- \(a_1\) es el primer elemento (cabeza ) y \(a_n\) el último (cola ).
- Decimos que \(a_i\) precede a \(a_{i+1}\) y \(a_i\) sucede a \(a_{i-1}\) y que \(a_i\) ocupa la posición i-ésima.
Listas. Operaciones básicas
- Insert (L, x, i) : añade el elemento x a la lista L en la posición i. Implica reorganizar los elementos de la lista.
- Append (L, x) : añade el elemento x al final de la lista L. Si se ha podido hacer devuelve el valor booleano true y si no false.
- Retrieve (L, i) : Devuelve el elemento en la posición iésima o null si no existe.
Listas. Operaciones básicas
- Delete (L, i) : Elimina el elemento de la posición iésima. Si se ha podido hacer devuelve el valor booleano true y si no false. Implica reorganizar los elementos de la lista.
- Length (L) : Devuelve \(|L|\), la longitud de L.
- Reset (L) : Hace que la posición actual sea igual la cabeza de la lista y devuelve el valor 1, si la lista está vacía devuelve 0.
Listas. Operaciones básicas
- Current (L) : Devuelve la posición actual en la lista L.
- Next (L) : Incrementa y devuelve la posición actual en la lista L.
Listas. Implementación
- Aprovechamos el uso de un LOO como es
C++. - Usaremos todos los términos en inglés.
Listas. Implementación
Cada TAD será una clase, p.e.:
typedef char Element; // Hasta que veamos genericidad // usaremos estos typedef. typedef int Position; class List { public: void insert (Element x, Position i); // Dónde está el primer // parámetro 'L'? ... }; List l; l.insert ('a', 1);
Listas. Implementación
- Diversas opciones para la representación interna.
- Puede ser un vector (array ).
Puede ser una serie de elementos en la cual cada uno sabe sólo cuál es su siguiente (simplemente enlazada ):

Figura 1: Lista simplemente enlazada.
Listas. Implementación
O también su anterior (doblemente enlazada ):

Figura 2: Lista doblemente enlazada.
Pilas
- Una pila es un tipo especial de lista.
- Sigue unas normas estrictas en lo referente a la inserción y extracción de elementos.
- Es una estructura LIFO (Last In, First Out ).
Pilas. Operaciones básicas
- Push (S, x) : Inserta x en S.
- Top (S) : Devuelve el último dato insertado en S (cabeza). Aplicada sobre una pila vacía lanzará una excepción de tipo EmptyStackException.
Pilas. Operaciones básicas
- Pop (S) : Elimina el último dato insertado en S (cabeza). En la práctica lo devuelve antes de eliminarlo. Aplicada sobre una pila vacía lanzará una excepción de tipo EmptyStackException.
- Empty (S) : Devuelve true si la pila no tiene elementos.
Ejemplo, apilamos A, B, C y desapilamos.
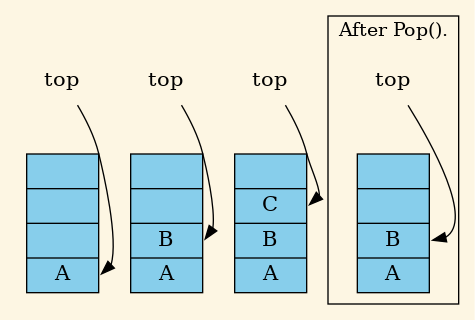
Figura 3: Apilar.
Pilas. Implementación
- Hemos dicho que son una Lista pero con ciertas restricciones.
- Podemos aprovechar el concepto de herencia de la POO.
¿Sería válida esta implementación de la clase
Pila?:class Stack : public List { public: void push (Element x); ... };
Pilas. Implementación
List* myList = new Stack();
myList->insert(0, value); // ¿Permitido? No debería en una pila.
Pilas. Implementación
¿Y esta?:
#include "list.h" class Stack : private List { public: void push (Element x); ... };
Pilas. Implementación
¿O esta otra?:
#include "list.h" class Stack { public: void push (Element x); ... private: List _l; };
Colas
- Una cola es un tipo especial de lista.
- Sigue unas normas estrictas en lo referente a la inserción y extracción de elementos.
- Es una estructura FIFO (First In, First Out ).
Colas. Operaciones básicas
- Enqueue (Q, x) : Inserta x en Q.
- Head (Q) : Devuelve el dato que más tiempo lleva en Q (cabeza). Aplicada sobre una cola vacía lanzará una excepción de tipo EmptyQueueException.
Colas. Operaciones básicas
- Dequeue (Q) : Elimina el dato que más tiempo lleva en Q (cabeza). Aplicada sobre una cola vacía lanzará una excepción de tipo EmptyQueueException.
Empty (Q) : Devuelve true si la cola no tiene elementos.
Por completitud, al dato que menos tiempo lleva en la cola se le llama
cola(del inglés tail ).
Colas. Operaciones básicas
Ejemplo, encolamos A, B, C y desencolamos.
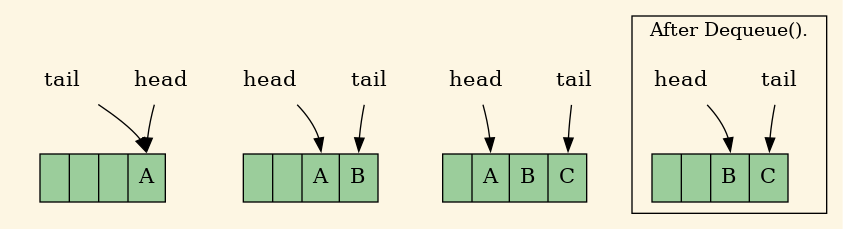
Figura 4: Encolar.
Colas. Implementación
- Hemos dicho que son una Lista pero con ciertas restricciones.
- Podemos aprovechar el concepto de herencia de la POO.
¿Sería válida esta implementación de la clase
Cola?:class Queue : public List { // Herencia pública. public: void enqueue (Element x); ... };
Colas. Implementación
¿Y esta?:
#include "list.h" class Queue : private List { // Herencia privada public: void enqueue (Element x); ... };
Colas. Implementación
¿O esta otra?:
#include "list.h" class Queue { public: void enqueue (Element x); ... private: List _l; // Composición };
Aclaraciones
- Este contenido no es la bibliografía completa de la asignatura, por lo tanto debes estudiar, aclarar y ampliar los conceptos que en ellas encuentres empleando los enlaces web y bibliografía recomendada que puedes consultar en la página web de la ficha de la asignatura y en la web propia de la asignatura.