




Next: #horne96j###:
Up: DTRNN based on threshold
Previous: #kremer95j###:
Contents
Index
The
work by Alon et al. (1991) (http://www.dlsi.ua.es/~mlf/nnafmc/papers/alon91efficient.pdf) stems
from the following consideration: if 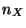 TLUs may be found in
TLUs may be found in 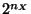 different states, ``one might wonder if an
different states, ``one might wonder if an 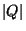 -state
FSM could be
implemented in a network with
-state
FSM could be
implemented in a network with 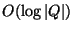 nodes''. These authors set out
to establish bounds on the smallest number of TLU needed to implement a
binary Mealy machine, that is, a Mealy machine with binary input and output
alphabets (
nodes''. These authors set out
to establish bounds on the smallest number of TLU needed to implement a
binary Mealy machine, that is, a Mealy machine with binary input and output
alphabets (
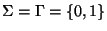 ), using a single-layer first-order
DTRNN architecture which is basically a neural Moore
machine (section 3.2.2) with threshold linear
units. The results
are far above the optimistic
), using a single-layer first-order
DTRNN architecture which is basically a neural Moore
machine (section 3.2.2) with threshold linear
units. The results
are far above the optimistic 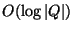 .
The main result presented by Alon et al. (1991) is that the number of units
necessary to implement a
.
The main result presented by Alon et al. (1991) is that the number of units
necessary to implement a 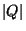 -state Mealy machine in such an architecture
is
-state Mealy machine in such an architecture
is
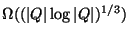 (lower bound to the
complexity)
and
(lower bound to the
complexity)
and
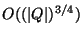 (upper bound to the complexity) when no restrictions
whatsoever are imposed on the fan-in or the
fan-out of the units or on the
values of weights. To obtain the lower bound, they use a counting argument
based on a lower bound on the number of ``really different'' Mealy
machines
of
(upper bound to the complexity) when no restrictions
whatsoever are imposed on the fan-in or the
fan-out of the units or on the
values of weights. To obtain the lower bound, they use a counting argument
based on a lower bound on the number of ``really different'' Mealy
machines
of 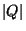 states and a lower bound on the number of different Mealy machines
that may be built using
states and a lower bound on the number of different Mealy machines
that may be built using 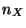 or less TLU. The upper bound is obtained by
construction but details are not given in the current paper.
However, reasonable (``mild'') restrictions on fan-ins, fan-outs and weights
lead to equal upper (
or less TLU. The upper bound is obtained by
construction but details are not given in the current paper.
However, reasonable (``mild'') restrictions on fan-ins, fan-outs and weights
lead to equal upper (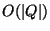 ) and lower (
) and lower (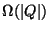 ) bounds.
) bounds.





Next: #horne96j###:
Up: DTRNN based on threshold
Previous: #kremer95j###:
Contents
Index
Debian User
2002-01-21