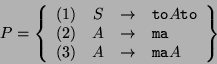Grammars provide a way to define languages by giving a finite set of rules that describe how the
valid strings may be
constructed. A grammar ![]() consists of: an alphabet
consists of: an alphabet ![]() of terminal symbols or terminals,
a finite set of variables
of terminal symbols or terminals,
a finite set of variables ![]() , a set of rewrite
rules
, a set of rewrite
rules ![]() or productions, and a start
symbol
or productions, and a start
symbol ![]() (a variable):
(a variable):
Rewrite rules or productions consist of a left-hand side ![]() and a right-hand side
and a right-hand side ![]() :
:
![]() .
Their meaning is: replace
.
Their meaning is: replace ![]() with
with ![]() .
.
Left-hand sides ![]() are strings over
are strings over ![]() , containing
at least one variable from
, containing
at least one variable from ![]() :
:
![]() . 5.1 Right-hand sides are strings over
. 5.1 Right-hand sides are strings over
![]() :
:
![]()
The grammar generates
strings in ![]() by
applying rewrite rules to the start symbol
by
applying rewrite rules to the start symbol ![]() until no
variables are left. Each time a rule is applied, a new sentential
form (string of variables from
until no
variables are left. Each time a rule is applied, a new sentential
form (string of variables from ![]() and terminals from
and terminals from ![]() )
is produced. For each rule
)
is produced. For each rule
![]() , any occurence of
a left-hand side
, any occurence of
a left-hand side ![]() as a subscript of the sentential form may be
substituted by
as a subscript of the sentential form may be
substituted by ![]() to form a new sentential form.
to form a new sentential form.
The language generated by the grammar, ![]() , is the set of
all strings that may be generated in that way. Recursive rewrite
rules,
that is, those which have the same variable in both the left-hand and
the right-hand side of a rule lead to infinite languages (if the
grammar has no useless symbols).5.2
, is the set of
all strings that may be generated in that way. Recursive rewrite
rules,
that is, those which have the same variable in both the left-hand and
the right-hand side of a rule lead to infinite languages (if the
grammar has no useless symbols).5.2
As an example, consider the following grammar,