Next: Nets with circles and
Up: Finite-state machines and neural
Previous: McCulloch and Pitts' neural
Contents
Index
What functions can a neuron compute?
From the statements in McCulloch and Pitts (1943) it follows
naturally that their neurons are equivalent to a model commonly used nowadays, where:
- Each neuron
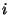 is in either of two states at time
is in either of two states at time 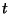 :
:
![$x_i[t]=1$](img16.png) or ``firing'' and
or ``firing'' and ![$x_i[t]=0$](img17.png) or ``not firing'';
or ``not firing'';
- all synapses (connections) are equivalent and characterized by a
real number (their strength), which is positive for excitatory
connections and negative for inhibitory
connections;
- a neuron
 becomes active when the sum of those connections
becomes active when the sum of those connections
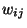 coming from neurons
coming from neurons 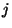 connected to it which are active,
plus a bias
connected to it which are active,
plus a bias 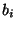 , is larger than zero.
, is larger than zero.
This is usually represented by
![\begin{displaymath}
x_i[t] =\theta\left( b_i + \sum_{j\in C(i)} w_{ij}
x_j[t-1]\right),
\end{displaymath}](img21.png) |
(3.1) |
where 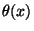 is the step function: 1 when
is the step function: 1 when
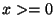 and 0 otherwise and
and 0 otherwise and 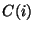 is the set of neurons that impinge
on neuron
is the set of neurons that impinge
on neuron 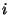 . This kind of neural processing
element is usually called a threshold
linear unit or TLU. The time indexes are dropped when processing
time is not an issue (Hertz et al., 1991, 4).
. This kind of neural processing
element is usually called a threshold
linear unit or TLU. The time indexes are dropped when processing
time is not an issue (Hertz et al., 1991, 4).
If all inputs (assume there are 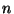 of them) to
a TLU are either 0 or 1, the neuron may be viewed as computing a
logical function of
of them) to
a TLU are either 0 or 1, the neuron may be viewed as computing a
logical function of 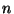 arguments. The truth
table of an arbitrary, total logical function of
arguments. The truth
table of an arbitrary, total logical function of 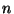 arguments has
arguments has
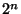 different rows, and the output for any of
them may be 0 or 1. Accordingly, there are
different rows, and the output for any of
them may be 0 or 1. Accordingly, there are 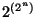 logical
functions of
logical
functions of 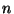 arguments. However, there are logical
functions a TLU cannot compute. For
arguments. However, there are logical
functions a TLU cannot compute. For 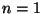 all
4 possible functions (identity, negation, constant true and constant
false) are computable. However,
for
all
4 possible functions (identity, negation, constant true and constant
false) are computable. However,
for 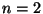 there are two noncomputable functions, corresponding to the
exclusive or and its negation. The
fraction of computable functions cannot be expressed as a closed-form
function of
there are two noncomputable functions, corresponding to the
exclusive or and its negation. The
fraction of computable functions cannot be expressed as a closed-form
function of 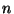 but vanishes as
but vanishes as 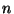 grows (Horne and Hush, 1996)). The
computable functions correspond to
those in which the set of all input vectors
corresponding to true outputs and the set of
all input vectors corresponding to false outputs are separable by a
grows (Horne and Hush, 1996)). The
computable functions correspond to
those in which the set of all input vectors
corresponding to true outputs and the set of
all input vectors corresponding to false outputs are separable by a
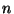 -dimensional hyperplane in that
-dimensional hyperplane in that 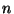 -dimensional space. This follows
intuitively from eq. (2.1): the equation of the hyperplane is
the argument of function
-dimensional space. This follows
intuitively from eq. (2.1): the equation of the hyperplane is
the argument of function 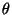 equated to zero.
equated to zero.
The computational limitations of TLUs have a radical consequence: to compute
a general logical function of 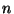 arguments, one needs a cascade of TLUs.
For example, to compute the exclusive-or function one needs at
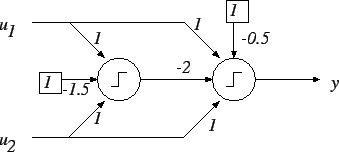
least two TLUs, as shown in figure 2.1.
arguments, one needs a cascade of TLUs.
For example, to compute the exclusive-or function one needs at
least two TLUs, as shown in figure 2.1.
Figure:
Two TLUs may be used to compute the
exclusive-or function
(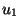 and
and 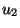 are the inputs,
are the inputs, 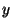 is the
output, and biases are
represented as connections coming from a constant input of 1).
is the
output, and biases are
represented as connections coming from a constant input of 1).
|
|
A common layout is the so-called multilayer perceptron
(MLP)
or layered feedforward neural net
(Haykin (1998), ch. 4; Hertz et al. (1991), ch. 6). In this layout:
- Each neuron belongs to a subset called layer.
- If neuron
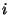 belongs to layer
belongs to layer 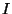 then all neurons
then all neurons 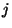 sending their output to neuron
sending their output to neuron 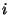 belong to layer
belong to layer 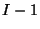 .
.
- Layer
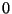 is the input
vector.
is the input
vector.
The backpropagation (BP) learning
algorithm
(Haykin (1998), sec. 4.3; Hertz et al. (1991), ch. 6) is usually formulated
for the MLP.





Next: Nets with circles and
Up: Finite-state machines and neural
Previous: McCulloch and Pitts' neural
Contents
Index
Debian User
2002-01-21
![]() of them) to
a TLU are either 0 or 1, the neuron may be viewed as computing a
logical function of
of them) to
a TLU are either 0 or 1, the neuron may be viewed as computing a
logical function of ![]() arguments. The truth
table of an arbitrary, total logical function of
arguments. The truth
table of an arbitrary, total logical function of ![]() arguments has
arguments has
![]() different rows, and the output for any of
them may be 0 or 1. Accordingly, there are
different rows, and the output for any of
them may be 0 or 1. Accordingly, there are ![]() logical
functions of
logical
functions of ![]() arguments. However, there are logical
functions a TLU cannot compute. For
arguments. However, there are logical
functions a TLU cannot compute. For ![]() all
4 possible functions (identity, negation, constant true and constant
false) are computable. However,
for
all
4 possible functions (identity, negation, constant true and constant
false) are computable. However,
for ![]() there are two noncomputable functions, corresponding to the
exclusive or and its negation. The
fraction of computable functions cannot be expressed as a closed-form
function of
there are two noncomputable functions, corresponding to the
exclusive or and its negation. The
fraction of computable functions cannot be expressed as a closed-form
function of ![]() but vanishes as
but vanishes as ![]() grows (Horne and Hush, 1996)). The
computable functions correspond to
those in which the set of all input vectors
corresponding to true outputs and the set of
all input vectors corresponding to false outputs are separable by a
grows (Horne and Hush, 1996)). The
computable functions correspond to
those in which the set of all input vectors
corresponding to true outputs and the set of
all input vectors corresponding to false outputs are separable by a
![]() -dimensional hyperplane in that
-dimensional hyperplane in that ![]() -dimensional space. This follows
intuitively from eq. (2.1): the equation of the hyperplane is
the argument of function
-dimensional space. This follows
intuitively from eq. (2.1): the equation of the hyperplane is
the argument of function ![]() equated to zero.
equated to zero.
![]() arguments, one needs a cascade of TLUs.
For example, to compute the exclusive-or function one needs at
least two TLUs, as shown in figure 2.1.
arguments, one needs a cascade of TLUs.
For example, to compute the exclusive-or function one needs at
least two TLUs, as shown in figure 2.1.